Einführung
Künstliche Neuronale Netze im Open Roberta Lab
Diese Anleitung richtet sich an Lehrkräfte und Personen, die bereits mit dem Open Roberta Lab und dem Begriff der Künstlichen Neuronalen Netze vertraut sind.

Künstliche Intelligenz verstehen
Wie funktioniert Künstliche Intelligenz?
Wie programmiere ich sie selbst?
Künstliche Intelligenz (KI) wird oft als komplexe Technologie wahrgenommen, die nur von Fachleuten verstanden und programmiert werden kann. Der wichtigste Teilbereich von KI sind Künstliche Neuronale Netze (KNN). Das Open Roberta Lab bietet Dir eine Möglichkeit, diese zu verstehen, zu programmieren, zu trainieren und zu testen. So kannst Du die Grundprinzipien von Künstlicher Intelligenz selbst erleben und anwenden.
#xNN
Künstliche Neuronale Netze heißen im Open Roberta Lab xNN – Explainable Neural Networks. Neuronale Netze werden oft als Blackbox wahrgenommen. Im Gegensatz dazu werden im Open Roberta Lab die scheinbar im Verborgenen stattfindenden Entscheidungen transparent gemacht, erklärt und veranschaulicht.
Künstliche Intelligenz verstehen
Wie funktioniert Künstliche Intelligenz?
Wie programmiere ich sie selbst?
Künstliche Intelligenz (KI) wird oft als komplexe Technologie wahrgenommen, die nur von Fachleuten verstanden und programmiert werden kann. Der wichtigste Teilbereich von KI sind Künstliche Neuronale Netze (KNN). Das Open Roberta Lab bietet Dir eine Möglichkeit, diese zu verstehen, zu programmieren, zu trainieren und zu testen. So kannst Du die Grundprinzipien von Künstlicher Intelligenz selbst erleben und anwenden.
#xNN
Künstliche Neuronale Netze heißen im Open Roberta Lab xNN – Explainable Neural Networks. Neuronale Netze werden oft als Blackbox wahrgenommen. Im Gegensatz dazu werden im Open Roberta Lab die scheinbar im Verborgenen stattfindenden Entscheidungen transparent gemacht, erklärt und veranschaulicht.
🤖 Künstliche Neuronale Netze in der Anwendung mit Robotern
Künstliche Neuronale Netze lassen sich im Open Roberta Lab nutzen, um einen Roboter selbstständig in seiner Umwelt zu bewegen. Das funktioniert folgendermaßen: Sensoren (z.B. Ultraschallsensoren als Entfernungsmesser) nehmen Informationen aus der Umgebung auf, leiten sie an das Neuronale Netz weiter und geben dessen Ergebnisse zurück an den Roboter, der mittels Aktoren (z.B. Motoren für die Bewegung) reagiert.
Wir benutzen dafür folgendes Beispiel:
Ein Roboter soll zu einem beweglichen Hindernis einen festen Abstand einhalten.
Das Neuronale Netz definieren
Zunächst wählen wir im Open Roberta Lab als System »Open Roberta xNN«. Im Reiter »NEURONALES NETZ Definieren« wird das Neuronale Netz erstellt. Es können Neuronen und verborgene Schichten erzeugt, Kantengewichte und Bias eingestellt sowie die gewünschte Aktivierungsfunktion ausgewählt werden.
Das erste Eingabe-Neuron soll die Werte des Ultraschallsensors (US) erhalten. Dann erstellen wir ein weiteres Eingabe-Neuron, nämlich unseren gewünschten Zielwert (Ziel) für die Entfernung. Das Ausgabe-Neuron nennen wir Tempo.
💡
Tipp
Das Programm
Anschließend schreiben wir ein Programm, das mit dem Neuronalen Netz zusammenarbeitet.
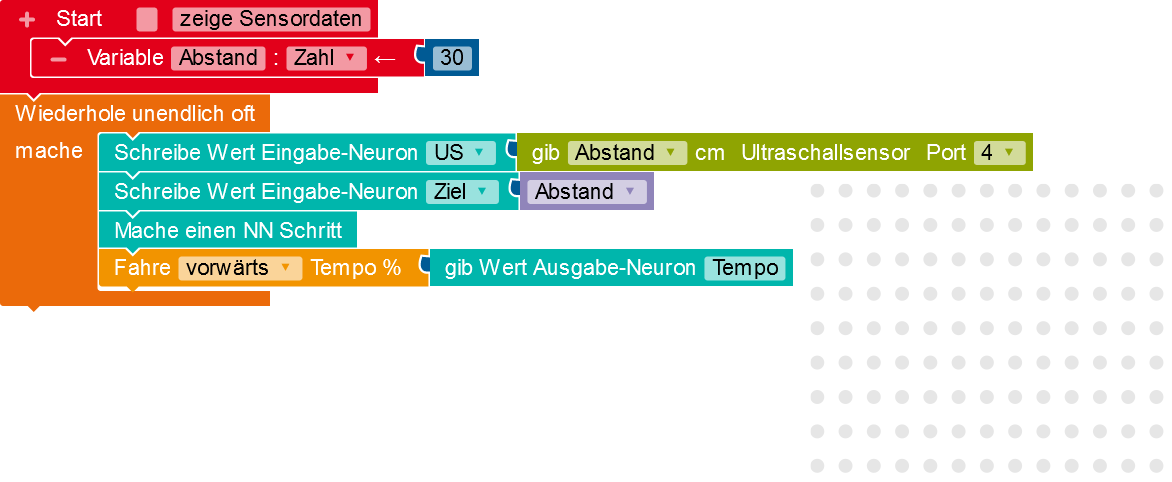
Was macht das Programm?
- Das Eingabe-Neuron US erhält als Eingabewert den Wert eines Ultraschallsensors am Roboter.
- Die Variable Abstand wird mit dem Wert 30 belegt und an das Eingabe-Neuron Ziel übergeben.
-
»Mache einen NN Schritt« nimmt die Werte der Eingabe-Neuronen und berechnet mithilfe des Neuronalen Netzes die Werte für die Ausgabe-Neuronen.
- Der Wert des Ausgabe-Neurons Tempo dient dann als Geschwindigkeitswert für die Fahrt des Roboters.
Kantengewichte und Bias einstellen
Jetzt stellen wir das Neuronale Netz so ein, dass der Roboter den Abstand von 30 cm zum Hindernis hält. Dazu weisen wir den Kanten den Wert 1 bzw. –1 sowie dem Bias des Ausgabe-Neurons den Wert 0 zu.
Wie berechnet sich der Wert des Ausgabe-Neurons Tempo?
- Die Berechnung des Werts an Tempo ergibt sich im Beispiel wie folgt:
Tempo = 1*US − 1*Ziel - Bei einem Abstand von mehr als 30 cm ergibt sich ein positiver Wert. Beispiel mit Abstand 70 cm: 1*70 − 1*30 = 40
- Bei einem Abstand von weniger als 30 cm ergibt sich dagegen ein negativer Wert. Beispiel mit Abstand 20 cm: 1*20 − 1*30 = −10
Die Simulation
Um unser Neuronales Netz zu testen, wechseln wir in die Simulation.
Was passiert in der Simulation?
- Im Beispiel erhält der Motorblock des Roboters den Wert des Ausgabe-Neurons Tempo.
- Dieser wird als Geschwindigkeitswert in % interpretiert.
- Ist der Wert positiv, fährt der Roboter vorwärts und hält an, wenn der vorgegebene Abstand zum Hindernis erreicht ist.
- Ist der Wert negativ, weil das Hindernis zu nahe ist, bewegt sich der Roboter rückwärts, bis der gewünschte Abstand wiederhergestellt ist.
Das Neuronale Netz trainieren
Wir haben gesehen, wie einfach es ist, ein Neuronales Netz zu nutzen, um unseren Roboter einen gewünschten Abstand zu einem beliebigen Hindernis einhalten zu lassen. Richtig interessant wird es aber, wenn wir das Neuronale Netz selbst lernen lassen, welche Werte (Kantengewichte und Bias) benötigt werden, um den gewünschten Abstand einzuhalten.
Neuronale Netze können lernen, indem sie mit Daten trainiert werden. Das ermöglicht es ihnen, komplexe Muster und Zusammenhänge zu erfassen, ohne dass diese explizit programmiert werden müssen. Beim Lernen wollen wir also nicht die Werte für die Kantengewichte und den Bias selbst festlegen, sondern diese durch Trainingsdaten, die wir definieren, bestimmen lassen.
1. Schritt & 2. Schritt
Zuerst wechseln wir wieder in den Reiter »NEURONALES NETZ Definieren« und weisen dieses Mal den Kanten und dem Bias des Ausgabe-Neurons zufällige Werte zu.
Anschließend wechseln wir in den Reiter »NEURONALES NETZ Lernen« und legen als Trainingsdaten die Eingabewerte und die dazu von uns erwarteten Ausgabewerte fest, die unser Neuronales Netz zum Lernen verwenden soll. Beispiel: Bei einem gemessenen Abstand von 100 cm (US = 100) und unserem Zielabstand von 30 cm soll das Netz einen Wert von 70 über das Ausgabe-Neuron Tempo ausgeben. Bei einem Wert von US = 30, soll das Ausgabe-Neuron einen Wert von 0 haben. Ist der gemessene Abstand kleiner als der Zielabstand und beträgt z.B. 10 cm, soll das Netz den Wert –20 als (negatives) Tempo ausgeben. Wie viele Werte wir eingeben, ist uns überlassen.
3. Schritt & 4. Schritt
Jetzt legen wir die Lernrate fest. Sie darf nicht zu klein sein, weil das Lernen sonst zu lange dauert. Sie darf aber auch nicht zu groß sein, weil sonst bisweilen keine Lösung gefunden werden kann. Durch Ausprobieren haben wir herausgefunden, dass 0,0003 ein guter Wert ist.
Dann starten wir den Lernprozess für unser Netz. Ziel ist es, das Netz so zu trainieren, dass es den erwarteten Werten so nahe wie möglich kommt. Sprich, das Trainingsloss soll möglichst klein, am besten nahe 0 sein. Ist das Trainingsloss zu groß, können die Epochenzahl erhöht bzw. die Lernrate angepasst werden. Durch Klick auf den Button »Starte/pausiere das Lernen des Netzes« lässt sich der Lernvorgang jederzeit unterbrechen, wenn der Trainingsloss bereits klein genug ist.
Wir wechseln wieder in die Simulation und überprüfen, ob unser trainiertes Neuronales Netz zu den gewünschten Ergebnissen führt. Wenn der Roboter sich nicht wie erwartet verhält, lassen wir das Netz im Reiter »NEURONALES NETZ Lernen« weiterlernen.
🎓
Was haben wir gelernt?
Wir haben gesehen, wie wir ein Neuronales Netz anlegen können, sodass unser Roboter einen Abstand von 30 cm zu einem Hindernis einhält. Dabei sind wir unterschiedlich vorgegangen.
Variante 1
Wir stellen die Wie-Frage
Wie kann ich die Kantengewichte so wählen, dass der Wert des Ausgabe-Neurons Tempo die gewünschte Motorengeschwindigkeit hat?
Dabei schauen wir in das Innere des Netzes. Lässt sich diese Frage einfach beantworten, werden Kantengewichte und Bias selbst festgelegt.
Variante 2
Wir stellen die Was-Frage
Was soll das Neuronale Netz machen und welche Trainingsdaten benötige ich dafür, damit der Roboter einen Abstand von 30 cm zu einem Hindernis einhält?
Wir schauen das Netz von außen an und konzentrieren uns auf das gewünschte Verhalten des Netzes. Dabei legen wir die Daten fest, die unseren Erwartungen entsprechen.
👉 Bei komplexen Beispielen ist es einfacher, sich zu überlegen, was das Neuronale Netz tun soll und welche Daten dafür benötigt werden, als festzulegen, wie dies geschehen soll.
🚀
Du kannst es nicht erwarten loszulegen?
Wechsel ins Open Roberta Lab und beginne mit dem Erstellen Deines eigenen Neuronalen Netzes. Und wenn Du mal nicht weiterkommst, helfen Dir unsere Einführungsmaterialien bestimmt weiter.
💡
Glossar zur Begriffserklärung
Aktivierungsfunktion
Die Aktivierungsfunktion ist eine mathematische Funktion in einem Neuronalen Netz, die die Ausgabe eines Neurons beeinflusst. Jedes Neuron in einem Neuronalen Netz nimmt Eingaben entgegen, gewichtet sie und wendet dann eine Aktivierungsfunktion auf die gewichtete Summe an, um die Ausgabe zu erzeugen. Es gibt verschiedene Arten von Aktivierungsfunktionen: Lineare Funktion, Sigmoidfunktion, Tanh, ReLU (Rectified Linear Unit).
Für die Arbeit im Open Roberta Lab bietet sich die lineare Funktion an. Sie führt bei einfachen Aufgaben zu guten Ergebnissen und eignet sich aufgrund der leichten Erklärbarkeit besonders für den Einstieg.
Backpropagation
Backpropagation ist ein Lernverfahren, das im Künstlichen Neuronalen Netz verwendet wird. Es hilft dem Netz, aus Fehlern zu lernen und seine Leistung zu verbessern. Die Anpassung der Gewichte erfolgt mit einem Optimierungsalgorithmus, der sicherstellt, dass das Netz die Gewichtungen und Bias-Werte so ändert, dass der Fehler reduziert wird.
Bias
Bias ist ein Wert, der zu den Eingaben und Gewichtungen eines Neurons hinzugefügt wird, bevor er durch eine Aktivierungsfunktion geht. Dieser zusätzliche Wert ermöglicht es dem Neuron, auch dann aktiviert zu werden, wenn alle Eingabewerte null sind. Bei manchen Aktivierungsfunktionen (z.B. ReLU) kann der Bias auch eine »hemmende Wirkung« haben. Hier wird das Neuron erst dann aktiviert, wenn ein bestimmter negativer »Schwellenwert« überschritten wird.
Epoche
In Bezug auf Neuronale Netze bezeichnet eine Epoche einen vollständigen Durchlauf aller Trainingsdaten während des Trainingsprozesses. In anderen Worten: Während einer Epoche sieht das Neuronale Netz jeden Trainingsdatensatz einmal.
Kantengewicht
Kantengewichte (auch einfach Gewichte genannt) sind Zahlen, die bestimmen, wie wichtig oder unwichtig die Verbindungen zwischen den Neuronen sind. Durch die Anpassung dieser Gewichte lernt das Netz, Daten richtig zu verarbeiten und Muster zu erkennen.
Während des Trainings (des Lernens) des Neuronalen Netzes werden diese Gewichte angepasst, um das Netz dazu zu bringen, die gewünschten Ausgaben für bestimmte Eingaben zu erzeugen. Der Lernprozess besteht darin, die Gewichte so zu optimieren, dass das Netz die richtigen Muster und Beziehungen in den Daten erkennt.
Lernrate
Die Lernrate ist wie die Größe der Schritte, die ein Computerprogramm macht, um zu lernen. Wenn die Lernrate hoch ist, lernt das Programm schnell, aber es könnte wichtige Dinge übersehen. Wenn die Lernrate niedrig ist, lernt das Programm genauer, aber es dauert länger. Es ist wichtig, die richtige Lernrate zu finden, damit das Programm gut und schnell lernt.
Neuron
Ein Neuron in einem Neuronalen Netz ist die grundlegende Recheneinheit, die Informationen verarbeitet. Es wird auch als »künstliches Neuron« oder »Perzeptron« bezeichnet. Ein Neuronales Netz besteht aus vielen solcher Neuronen, die in Schichten angeordnet sind.
Das künstliche Neuron nimmt Eingaben entgegen (Eingabe-Neuron), multipliziert sie mit bestimmten (Kanten-)Gewichten, addiert sie und wendet auf das Ergebnis eine Aktivierungsfunktion an. Die Aktivierungsfunktion bestimmt, ob und wie stark das Neuron aktiviert wird und welche Informationen es an die nächsten Neuronen weitergibt, bis die Information über Ausgabe-Neuronen zur Verfügung steht.
Trainingsloss
Das Trainingsloss (auch Trainingsverlust genannt) ist ein Maß dafür, wie gut ein Neuronales Netz während des Trainings Aufgaben löst. Es misst den Unterschied zwischen den vorhergesagten Ausgaben des Netzes und den tatsächlichen Zielwerten (auch Labels genannt) für die Trainingsdaten. Trainingsloss ist eine Art »Fehler«, der angibt, wie weit die Vorhersagen des Neuronalen Netzes von den tatsächlichen Werten entfernt sind. Während des Trainingsprozesses wird versucht, dieses Loss zu minimieren, indem die Gewichtungen und Bias-Werte des Netzes angepasst werden.
Verborgene Schicht
Ein Neuronales Netz kann in Schichten eingeteilt werden. Die erste Schicht erhält Eingaben (Werte) über die Eingabe-Neuronen, die letzte gibt Ausgaben (Werte, die als Wahrscheinlichkeiten interpretiert werden, die sogenannten Ausgabe-Neuronen) aus. Dazwischen gibt es »versteckte« bzw. »verborgene« Schichten, weil wir ihre Arbeit nicht direkt sehen können. Diese verborgenen Schichten lernen, komplexe Muster in den Daten zu verstehen, indem sie Eingaben miteinander kombinieren. Sie sind wichtig, um schwierige Probleme zu lösen. Die Anzahl und Größe dieser versteckten Schichten beeinflussen, wie gut das Netz funktioniert.
Dir fehlt ein Begriff? Dann schreib uns gerne eine E-Mail.
📄
Einführungs- und Übungsmaterialien zu Neuronalen Netzen

Künstliche Neuronale Netze mit dem Open Roberta Lab
Diese Folien bieten Dir einen ersten Einstieg in die Programmierung eigener Künstlicher Neuronaler Netze mit dem Open Roberta Lab.

Programmieren eines Roboters mit xNN
Diese Folien bieten Dir Praxisbeispiele für die Programmierung eines Roboters mithilfe Neuronaler Netze.
